1. 딥러닝(Deep Learning)의 기초
딥러닝은 인간의 신경망을 모방하여 설계된 알고리즘으로, 주로 신경망(Neural Network)을 통해 데이터를 처리하고 학습한다.
퍼셉트론(Perceptron):
- 신경망의 가장 기본 단위.
- 선형 데이터를 처리할 수 있지만, 비선형 문제(XOR 등)는 해결하지 못한다.
다층 퍼셉트론(MLP, Multi-layer Perceptron):
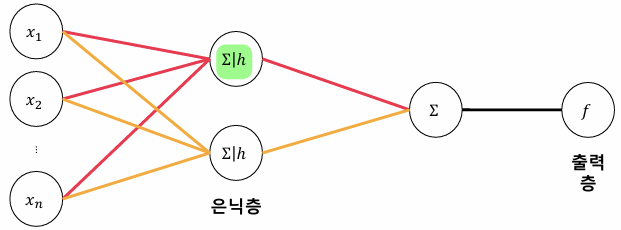
- 여러 은닉층(Hidden Layer)을 쌓아 비선형 데이터를 처리 가능.
- 활성화 함수(Activation Function)를 통해 비선형성을 부여한다.
은닉층(Hidden Layer):

- 새로운 특징을 추출하는 함수.
활성화 함수(Activation Function):
- 출력 범위와 기울기 소멸 문제를 해결하기 위해 설계됨.

- Sigmoid는 출력값을 0에서 1 사이로 제한하지만, 입력값이 큰 경우 기울기가 0에 가까워지는 문제가 있다.
- Tanh는 출력값을 −1에서 1 사이로 제한하며, Sigmoid보다 학습이 빠르지만 여전히 기울기 소멸 문제가 있다.
- ReLU는 음수 입력을 0으로, 양수 입력을 그대로 출력하여 계산 효율성이 높다. 다만, Dying ReLU 문제가 발생할 수 있다.
- Leaky ReLU는 음수 입력에서도 작은 기울기를 유지하여 Dying ReLU 문제를 완화한다.
UAT (Universal Approximation Theorem): 하나의 은닉층을 가진 MLP도 적절한 뉴런 수와 활성화 함수가 있다면 임의의 연속 함수에 근사할 수 있다.
2. 역전파(Backpropagation)와 최적화(Optimization)
역전파(Backpropagation)

역전파는 신경망 학습 과정에서 손실 함수의 값을 줄이기 위해 기울기를 계산하고 가중치를 업데이트하는 알고리즘이다.
- 개념: 출력층에서 계산된 손실 값을 입력층 방향으로 거슬러 올라가며 각 층의 기울기를 계산한다.
- 기울기 계산: 각 뉴런의 가중치에 대해 손실 함수의 편미분 값을 계산한다.
수식
- 손실 함수 \(L\)의 출력값 \(\hat{y}\)에 대한 편미분:
$$\frac{\partial L}{\partial \hat{y}}$$ - 출력값 \(\hat{y}\)와 가중치 \(W\) 사이의 관계를 통해 편미분을 전파:
$$\frac{\partial L}{\partial W} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial W}$$ - 반복적으로 각 층의 가중치와 편미분 계산:
$$W_{new} = W - \eta \cdot \frac{\partial L}{\partial W}$$
여기서 \(\eta\)는 학습률(Learning Rate)이다.
손실 함수(Loss Function)
손실 함수는 모델의 예측 값 \(\hat{y}\)와 실제 값 \(y\) 간의 차이를 수치화하는 함수이다.
- Cross-Entropy: 분류 문제에서 사용되며, 두 확률 분포 \(P\)와 \(Q\)간의 차이를 계산한다.
$$L = - \sum_{i=1}^N y_i \log(\hat{y}_i)$$ - Mean Squared Error (MSE): 회귀 문제에서 사용되며, 실제 값과 예측 값의 차이를 제곱한 평균을 계산한다.
$$L = \frac{1}{N} \sum_{i=1}^N (y_i - \hat{y}_i)^2$$
경사 하강법(Gradient Descent)
경사 하강법은 손실 함수의 기울기를 따라 가중치를 업데이트하며 손실을 최소화하는 최적화 알고리즘이다.
- SGD (Stochastic Gradient Descent)는 작은 배치 데이터에 대해 경사를 계산하여 빠른 학습을 지원한다.
- Adam Optimizer는 학습률을 동적으로 조정하여 SGD보다 안정적으로 수렴한다.
$$W_{t+1} = W_t - \eta \cdot \nabla L(W_t)$$
여기서 \(W_t\)는 현재 가중치, \(\eta\)는 학습률, \(\nabla L\)은 손실 함수의 기울기이다.
3. 딥러닝 프레임워크
- TensorFlow: Google에서 개발한 프레임워크로, 모델 배포(TensorFlow Lite, Serving)와 정적 그래프 활용에 강점이 있다.
- PyTorch: Meta에서 개발한 프레임워크로, Pythonic한 코드와 동적 그래프를 제공하여 연구에 적합하다.
- JAX: Google이 개발한 프레임워크로, 속도와 최적화가 뛰어나지만 생태계가 아직 작다.
4. 실습: Multi-Layer Perceptron(MLP)를 이용한 Image Classification
더보기
간단한 실습 과정이므로 코드는 생략함.
1. Iris 데이터셋
- 모델 구조
- 입력층: Iris 데이터의 4개 특징.
- 은닉층: ReLU 활성화 함수와 5개 뉴런.
- 출력층: 3개 클래스 분류.
- 학습 프로세스
- 손실 함수: Cross-Entropy Loss.
- 최적화: SGD (학습률 0.1).
- 학습: 샘플 데이터를 입력받아 100번 반복 학습.
- 결과
- 손실 감소 확인.
- 은닉층의 뉴런 수를 증가시킬수록 더 낮은 손실 달성 가능.
- 오버피팅 발생 가능성 확인.
2. MNIST 데이터셋
- 데이터 전처리
- 28x28 이미지 데이터를 784 차원의 1D 벡터로 변환 후 Binary 형태로 시각화.
- Cross-Entropy Loss 사용.
- 모델 구조
- 입력층: 784개의 뉴런.
- 은닉층: 1000개의 뉴런과 ReLU 활성화 함수.
- 출력층: 10개의 클래스.
- 학습 프로세스
- SGD를 이용해 100번 학습 반복.
- 첫 5개 샘플에 대해 예측 결과 확인.
결론
딥러닝은 데이터를 통해 복잡한 패턴을 학습하고, 다양한 문제를 해결하는 데 정말 강력한 도구라는 점을 확인할 수 있었다. 이번 실습을 통해 MLP의 기본 구조와 PyTorch를 활용하는 방법을 배우며, 활성화 함수와 최적화 방법이 얼마나 중요한지 느낄 수 있었다. 특히, 은닉층의 뉴런 수와 모델의 복잡도가 성능에 큰 영향을 미친다는 점을 알게 되었고, 앞으로 딥러닝을 활용한 실험에서 과적합을 방지하고 모델의 일반화 성능을 높이는 방법에 대해 더 깊이 고민해봐야겠다는 생각이 들었다.
'Theory > DL & Medical AI' 카테고리의 다른 글
| [딥러닝을 활용한 의료 영상 처리 & 모델 개발] Part2-2. Medical image acquisition & preprocessing (0) | 2025.01.02 |
|---|---|
| [딥러닝을 활용한 의료 영상 처리 & 모델 개발] Part2-1. Medical image file format (0) | 2025.01.02 |
| [딥러닝을 활용한 의료 영상 처리 & 모델 개발] Part1-4. GAN, RNN, Transformer (3) | 2024.12.27 |
| [딥러닝을 활용한 의료 영상 처리 & 모델 개발] Part1-3. Convolutional Neural Network (0) | 2024.12.27 |
| [딥러닝을 활용한 의료 영상 처리 & 모델 개발] Part1-1. Machine Learning (2) | 2024.12.27 |