1. Image Classification
- 정의:
- 주어진 이미지를 특정 카테고리로 분류하는 작업.
- 컴퓨터 비전에서 객체 탐지, 영역 분할 등의 확장된 작업으로 이어질 수 있음.
- Challenges:
- 이미지의 다양한 변형과 외부 요인:
- 시점 변화(Viewpoint variation): 다양한 각도에서 촬영된 이미지.
- 크기 변화(Scale variation): 객체 크기의 변동.
- 변형(Deformation): 이미지 왜곡, 회전.
- 외부 요인: 조명(Illumination conditions), 가림(occlusion), 배경의 다양성(Background clutter).
- 이미지의 다양한 변형과 외부 요인:
- Image classification model:
- Convolutional Neural Network (CNN):
- 이미지 데이터를 3차원 텐서(RGB 채널)로 처리.
- 주요 모델: ResNet, DenseNet, EfficientNet.
- Vision Transformer (ViT):
- 이미지를 패치로 분리하고 Position Embedding을 추가.
- 주요 모델: DeiT, BEiT.
- Convolutional Neural Network (CNN):
2. Medical Image Classification
- Medical image classification tasks
- Category Label(Classification):
- 이진 분류: 양성/악성.
- 다중 클래스 분류: 병리학적 상태.
- Continuous Value(Regression):
- 연속 값 예측(예: 질병의 심각도).
- Category Label(Classification):

- ML Medical image classification tasks:
- Wavelet Frame Transform과 Fuzzy C-Means
항목 Wavelet Frame Transform Fuzzy C-Means 기본 목적 주파수와 시간 영역에서 데이터의 특징 추출. 데이터를 여러 클러스터로 분리. 적용 대상 신호 처리 및 이미지의 지역적 특징 분석. 데이터 포인트 간의 유사성을 기반으로 클러스터링. 결과물 Edge, Texture 같은 특징 데이터. 각 데이터의 소속 확률 및 클러스터 중심.
- Wavelet Frame Transform과 Fuzzy C-Means
- ML Feature Extractor:
- 기존 Texture, Shape feautre를 뽑아냄.
- 나이브 베이즈 (Naive Bayes):
- 조건부 확률과 독립성 가정을 기반으로 간단하고 빠르게 분류.
- 독립성 가정이 현실적이지 않을 경우 성능 저하 가능.
- 의사결정트리 (Decision Trees):
- 데이터를 분기 기준으로 트리 구조로 분류하며, 직관적이고 해석이 쉬움.
- 과적합 문제와 데이터 변동에 민감.
- 선형 분류 (Linear Classification):
- 선형적으로 구분 가능한 데이터를 빠르고 간단하게 분류.
- 비선형 데이터 처리에는 부적합.
- 최근접이웃 (K-Nearest Neighbors, KNN):
- 입력 데이터를 가장 가까운 K개의 이웃으로 분류하며, 단순한 구조에 적합.
- 계산량이 많아 대규모 데이터에서 비효율적.
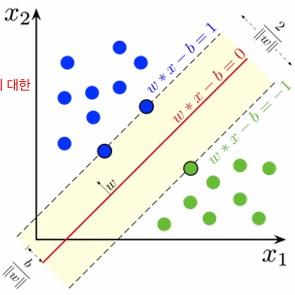
- 서포트 벡터 머신 (SVM):
- 클래스 간 마진을 최대화하며 decision boundary를 만들어 고차원 데이터와 비선형 문제에 강점.
- 데이터 크기와 커널 선택에 민감.
- DL의 필요성:
- 전통적인 Feature Extraction 방식의 한계를 극복.
- 딥러닝 모델은 Feature Extraction과 예측 과정을 통합.
- Challenges:
- Limited data → Fine tuning
- Large data → Crop
- Demographic score → Multi label (regression)
- DL 학습 방식:
- Transfer Learning:
- Pretrained 모델 활용 후 Fine-tuning.
- CNN + ML 연계:
- CNN으로 특징을 추출하고 머신러닝 모델에서 분류.
- CNN + Fully Connected Layer:
- CNN 이후 FC 레이어에서 최종 분류 수행.
- Scratch:
- 모델을 처음부터(초기화된 상태에서) 학습시키는 방식.( vs Transfer Learning)
- Transfer Learning:
- DL Feature Extractor
- Binary classification: 질병 유무 분류(class = 1).
- ex) MRI: 알츠하이머 병 진단 (True, False)
- Multi label classification: 질병 타입 분류.
- Softmax 사용.
- ex) Lung CT: Normal, Emphysema, Ground glass, Fibrosis
- Multi class classification: 한 개의 이미지에 중복된 label이 있는 경우.
- Sigmoid 사용(Softmax X).
- Binary classification: 질병 유무 분류(class = 1).
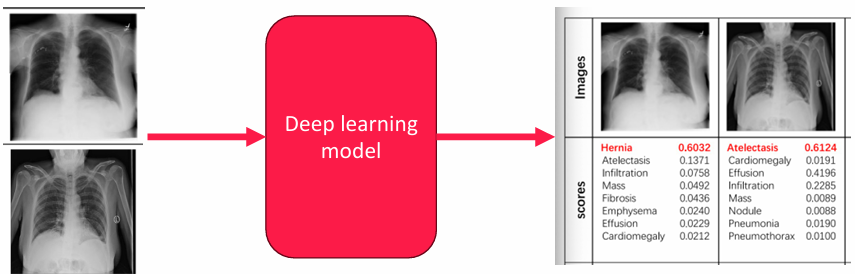

- ML vs DL Feature Extractor
항목 ML Feature Extractor DL Feature Extractor Feature Extraction 수작업으로 정의된 특징(Shape, Texture 등) 사용 모델이 특징을 자동으로 학습 사전 처리 필요성 수작업으로 특징 추출 및 가공 필수 원본 데이터를 바로 입력 가능 데이터 의존성 데이터셋 크기가 작아도 잘 작동 대규모 데이터셋에서 성능이 더 우수 복잡성 간단한 데이터 구조와 문제에 적합 복잡한 데이터와 비선형 문제 처리 가능 알고리즘 적용 KNN, SVM, Decision Tree 등 사용 CNN, ViT, ResNet 등 딥러닝 모델 사용
- Medical image classification trick:
- Many augmentation
- Large batch data
- Learning rate
- Other model
- Loss Functions
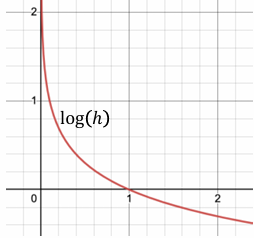
- Binary Cross Entropy (BCE)
- 특정 질병의 유무를 판단하기 위한 손실 함수.
- $BCE = - \frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(h(x_i)) + (1 - y_i) \log(1 - h(x_i)) \right]$
- $y_i$: 실제 값 (0 또는 1).
- $h(x_i)$: 예측 확률.
- 특징:
- 양성일 때는 $y_i \log(h(x_i))$가 최소화.
- 음성일 때는 $(1 - y_i) \log(1 - h(x_i))$가 최소화.
- 확률값 $h(x_i)$가 실제 클래스에 가까워질수록 손실 감소.
- Cross Entropy
- 다중 클래스 분류를 위한 손실 함수.
- $CE = - \frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{M} y_{ij} \log(h_j(x_i))$
- MM: 클래스의 총 개수.
- $y_{ij}$: $i$-번째 샘플이 $j$-번째 클래스에 속하는지 여부.
- $h_j(x_i)$: $i$-번째 샘플의 $j$-번째 클래스에 대한 예측 확률.
- 특징:
- 각 클래스의 예측 확률과 실제 레이블의 분포 차이를 최소화.
- 클래스별 확률을 0 또는 1에 가깝게 조정.
- Kullback-Leibler Divergence (KL Divergence)
- 예측 분포와 실제 분포 간의 차이를 측정.
- $D_{KL}(P || Q) = \sum_{x \in X} P(x) \log\left(\frac{P(x)}{Q(x)}\right)$
- $P(x)$: 실제 분포.
- $Q(x)$: 예측 분포.
- 특징:
- 두 분포를 가깝게 만들어 학습하도록 유도.
- 분류 모델에서 분포 차이를 최소화하는 데 사용.
- Binary Cross Entropy (BCE)


3. Image Regression
- 정의:
- 이미지를 입력받아 연속적인 값을 예측.


- Traditional image regression method:
- Regression Trees:
- Decision Tree Regression:
- 작동 원리:
- 데이터를 반복적으로 분할하여 트리 구조로 예측.
- 각 분기는 데이터의 특징을 기준으로 분리하여 최종적으로 연속적인 값을 예측.
- 특징:
- 직관적이고 해석이 용이.
- 단일 트리로 학습하면 과적합 위험이 있음.
- Random Forest:
- 작동 원리:
- 여러 개의 Decision Tree를 생성하고 결과를 평균(Voting)하여 최종 예측.
- Bagging(부트스트랩 샘플링)으로 각 트리를 독립적으로 학습.
- 특징:
- 과적합을 방지하고 모델의 안정성을 높임.
- 다수의 트리를 사용하므로 계산 비용이 증가.
- 작동 원리:
- Gradient Boosting:
- 작동 원리:
- 각 Decision Tree가 이전 모델의 오차(Residual)를 학습하도록 설계.
- 앙상블 모델로, 약한 학습기(Weak Learner)를 조합하여 강력한 예측기 생성.
- 특징:
- 높은 예측 성능.
- 학습 속도가 느리고, Hyperparameter Tuning이 중요.
- XGBoost (Extreme Gradient Boosting)
- 특징:
- Gradient Boosting을 개선한 모델로, 병렬 처리 및 Regularization 지원.
- Regression과 Classification 모두 사용 가능.
- Hyperparameter Tuning을 통해 성능 최적화 가능.
- 주요 기능:
- Overfitting 방지를 위한 Regularization(L1, L2).
- 병렬 처리를 통해 학습 속도 향상.
- Tree Pruning과 같은 기능으로 모델 최적화.
- 특징:
- 작동 원리:
- Regression Trees:


4. Medical Image Regression
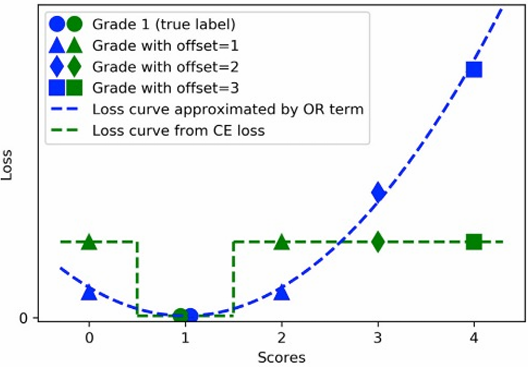
- 정의
- 질병의 중증도(Grading)나 병변 크기와 같은 연속적인 값 예측.
- Threshold 사용:
- 특정 값을 기준으로 예측 결과를 구분.
- 예: 0~1의 스코어로 중증도를 정량화.
- Ex) Diabetic retinopathy (DR) / Lung CT

- Medical image regression trick:
- K fold cross validation:
- 데이터를 K개의 폴드(Fold)로 나누어 학습과 평가를 반복.
- 모델의 일반화 성능 평가에 유리.
- imbalanced data:
- Oversampling: 소수 클래스 데이터를 증강(SMOTE 등).
- Undersampling: 다수 클래스 데이터를 감소.
- Augmentation
- K fold cross validation:

- Loss Functions:
- L1 Loss: $$L1 = \sum_{i=1}^{N} |y_i - \hat{y}_i|$$
- 예측값($\hat{y}_i$)과 실제값($y_i$)의 절댓값 차이를 계산.
- Outlier에 강건(Robust).
- 미분이 안되는 지점 존재.
- L2 Loss (MSE):
- $$L2 = \sum_{i=1}^{N} (y_i - \hat{y}_i)^2$$
- 제곱 오차를 계산하여 안정적이나 Outlier에 민감.
- Huber Loss:
- $$Huber = \begin{cases} \frac{1}{2}(y_i - \hat{y}_i)^2 & \text{if } |y_i - \hat{y}_i| \leq \delta \\ \delta \cdot (|y_i - \hat{y}_i| - \frac{\delta}{2}) & \text{if } |y_i - \hat{y}_i| > \delta \end{cases}$$
- L1과 L2 Loss의 장점을 결합.
- Outlier에 Robust하면서 미분 가능.
- Smooth L1 Loss:
- $$\text{Smooth L1 Loss} = \frac{1}{N} \sum_{i=1}^{N} \text{loss}(x_i, y_i)$$
-
- xix_i: 예측값.
- yiy_i: 실제값.
- δ\delta: 임계값(Huber Threshold).
- Huber Loss와 유사하며 모든 지점에서 미분 가능.
- L1보다 안정적이며, L2보다 Outlier에 Robust
- L1 Loss: $$L1 = \sum_{i=1}^{N} |y_i - \hat{y}_i|$$




5. Classification & Regression evaluation metric
- Classification Eval
- 혼동행렬(Confusion Matrix):
- True Positive (TP): 실제 Positive를 올바르게 예측.
- False Positive (FP): 실제 Negative를 Positive로 잘못 예측.
- True Negative (TN): 실제 Negative를 올바르게 예측.
- False Negative (FN): 실제 Positive를 Negative로 잘못 예측.
- 혼동행렬(Confusion Matrix):

- 기본 지표:
- Accuracy: $Accuracy = \frac{TP + TN}{TP + FP + FN + TN}$
- Precision (정밀도): $Precision = \frac{TP}{TP + FP}$
- Recall (재현율): $Recall = \frac{TP}{TP + FN}$
- Specificity (특이도): $Specificity = \frac{TN}{TN + FP}$
- 추가 지표:
- F1 Score: $$F1 = 2 \times \frac{Precision \times Recall}{Precision + Recall}$$
- AUROC (Area Under ROC Curve):
- ROC Curve 아래 면적을 사용하여 모델 성능 평가.
- $\text{TPR} = \frac{TP}{TP + FN}, \text{FPR} = \frac{FP}{FP + TN}$


- Cohan Kappa
- 정의:
- 두 평가자 간 일치도를 측정.
- -1에서 1 사이의 값을 가지며, 1은 완벽한 일치, 0은 무작위 일치.
- 수식:$\frac{P_o - P_e}{1 - P_e}$
- $P_o$: 관찰된 일치도.
- $P_e$: 우연에 의한 기대 일치도.
- 정의:

- Pearson correlation
- 정의:
- 두 변수 간의 선형 상관관계를 측정.
- 수식: $\frac{\sum_{i=1}^{N} (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{N} (X_i - \bar{X})^2} \cdot \sqrt{\sum_{i=1}^{N} (Y_i - \bar{Y})^2}}$
- $X_i, Y_i$: 각각의 관측값.
- $\bar{X}, \bar{Y}$: X와 Y의 평균값.
- 특징:
- -1: 완벽한 음의 상관관계.
- 0: 상관관계 없음.
- 1: 완벽한 양의 상관관계.
- 의료 영상 응용:
- 병변 크기와 질병 중증도 간의 관계를 분석.
- 정의:

4. Prostate cANcer graDe Assessment(PANDA) Challenge 실습
코드 리뷰 링크: [딥러닝을 활용한 의료 영상 처리 & 모델 개발] Part2-4. Prostate cANcer graDe Assessment(PANDA) Challenge 실습 1~3
[딥러닝을 활용한 의료 영상 처리 & 모델 개발] Part2-4. Prostate cANcer graDe Assessment(PANDA) Challenge 실습
prostate-cancer-grade-assessment(데이터셋 생성): https://github.com/ahxlzjt/MedImagingDL/blob/0583fd20671f79a2785bc398da0b2ca2f1c1cc51/ch04_05_prostate_cancer_grade_assessment.ipynb MedImagingDL/ch04_05_prostate_cancer_grade_assessment.ipynb at 0583
ahxlzjt.tistory.com
5. 결론
이론은 확실히 배웠던거라 쉬웠다. Classification이나 Regression의 개념, 그리고 Evaluation Metrics는 기본적으로 직관적이라 이해하는 데 큰 어려움은 없었다. Precision, Recall, MSE 같은 지표는 개념적으로 명확했고, 각 알고리즘의 특징도 비교적 간단하게 정리됐다.
근데 Prostate cANcer graDe Assessment(PANDA) Challenge 실습 들어가면서부터 얘기가 달라졌다. 데이터 전처리부터 모델 구현까지 하나하나가 복잡했고, 특히 고해상도 병리학 데이터를 다루는 과정이 생각보다 만만치 않았다. Challenge 코드라 그렇겠지.. 나중엔 주석만 보고도 해석하기 쉽기를..