[OUTTA Alpha팀 논문 리뷰 요약] Part 5-5. DDPM: DENOISING DIFFUSION IMPLICIT MODELS

논문 링크: 2010.02502

 

OUTTA 논문 리뷰 링크: [2025-1] 임재열 - DDPM(Denoising Diffusion Probabilistic Models)

[2025-1] 임재열 - DDPM(Denoising Diffusion Probabilistic Models)

---

1. Introduction

• DDPM (Denoising Diffusion Probabilistic Models):
  • Markov Chain 기반 생성 모델로, Forward와 Reverse 두 과정으로 구성.
    • 각 단계에서 이전 단계의 값만 참조하여 확률 분포를 계산: $$q(x_t | x_{t-1}), \quad p_\theta(x_{t-1} | x_t)$$

• DDPM의 차별점:
  • Forward Process: 데이터 분포를 점차 단순화하며 Gaussian 분포로 변환.
  • Reverse Process: 단순화된 Gaussian 분포에서 데이터를 복원.
  • 기존 GAN 대비 안정적 학습과 높은 품질의 이미지 생성.

---

2. Background

2.1 Forward-Backward 관계

• Forward와 Reverse는 Markov Chain 관계를 기반으로 설계: $$q(x_{1:T} | x_0) = \prod_{t=1}^T q(x_t | x_{t-1})$$
  • $q(x_t | x_{t-1})$: Forward에서 $t-1$ 단계에서 $t$ 단계로 데이터 변환.
  • Reverse 과정은 $p_\theta(x_{t-1} | x_t)$로 모델링.

2.2 Variational Lower Bound

• Reverse Process를 학습하기 위해 변분 추정(Variational Inference) 사용: $$\log p_\theta(x_0) \geq \mathbb{E}_q \left[ \log p_\theta(x_{0:T}) - \log q(x_{1:T} | x_0) \right]$$
  • Forward와 Reverse 간의 KL 발산을 최소화하는 방식으로 학습.

2.3 Noise Schedule $B(t)$

• Forward Process에서 노이즈 강도를 조절하는 스케줄링:
  • $B(t)$는 각 단계의 노이즈 강도를 결정.
  • $\beta_t$: 선형, Quadratic, Sigmoid 방식으로 증가 가능.
    • Linear: 일정한 증가율.
    • Quadratic: 부드러운 학습률 변화와 더 유연한 노이즈 조절.
    • Sigmoid: 초기에 느리고 마지막에 빠르게 증가.

---

3. Methodology

3.1 Forward Diffusion Process

• 목적: 데이터 $x_0$​에 노이즈를 점진적으로 추가해, 순수 Gaussian 노이즈 $x_T$​로 변환.
• 수식: $$q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I)$$
  • $\beta_t$​: 시간 $t$에서의 노이즈 강도.
  • 데이터 분포가 점진적으로 단순 Gaussian 분포에 가까워짐.
• 누적 샘플링: $$q(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I)$$
  • $\bar{\alpha}_t = \prod_{i=1}^t (1 - \beta_i)$

3.2 Reparameterization Trick

• Forward에서 $x_t$​를 직접 샘플링하지 않고 $x_0$​와 노이즈 $\epsilon \sim \mathcal{N}(0, I)$를 사용: $$x_t = \sqrt{\bar{\beta}_t} x_0 + \sqrt{1 - \bar{\beta}_t} \epsilon$$
• 장점:
  • 샘플링 과정을 단순화.
  • 모델 학습 효율성 증대.

3.3 Reverse Diffusion Process

• 목적: 순수 노이즈에서 시작해 점진적으로 노이즈를 제거하며 원본 데이터 복원.
• 수식: $$p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))$$
  • $\mu_\theta$​: 학습된 평균.
  • $\Sigma_\theta$​: 학습된 분산.
• Reverse Process는 Neural Network로 모델링되어 학습.

3.4 손실 함수

• 목표: Forward와 Reverse 과정에서의 분포 차이를 최소화.
• 수식: $$L = \mathbb{E}_q \left[ \sum_{t=1}^T w_t \| \epsilon - \epsilon_\theta(x_t, t) \|^2 \right]$$
  • $w_t$​: 각 단계별 가중치.
  • $\epsilon$: Forward 과정에서 추가된 노이즈.
  • $​\epsilon_\theta$: 모델이 추정한 노이즈.

---

4. Reverse Process와 U-Net

4.1 U-Net의 역할

• Reverse 과정에서 $\epsilon_\theta(x_t, t)$를 추정하는 데 사용.
• 구조:
  • Encoder-Decoder 기반.
  • Skip Connection으로 다중 스케일 특징 유지.
• 시간 정보 반영:
  • 시간 $t$를 Fourier Embedding으로 변환해 네트워크에 전달: $$t_{emb} = \text{sinusoidal embeddings of } t$$

4.2 Reverse Process

• U-Net을 사용해 각 단계에서 노이즈를 제거: $$\epsilon_\theta(x_t, t) \approx \epsilon$$

---

5. 실험 결과 및 분석

5.1 데이터셋

 

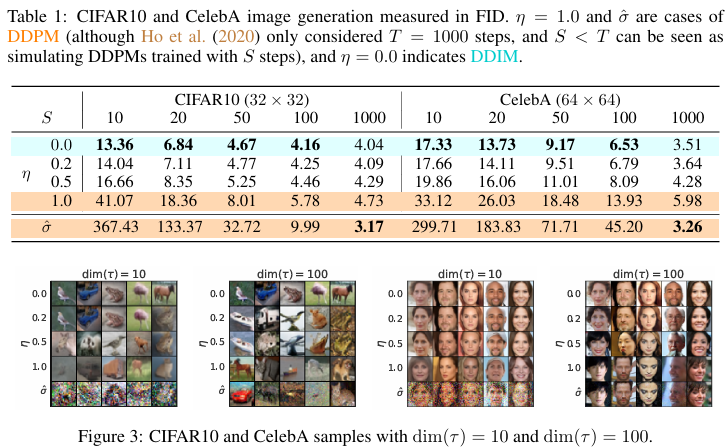
• CIFAR-10, CelebA, LSUN, ImageNet 등에서 실험.

5.2 성능 비교

• FID (Fréchet Inception Distance) 기준에서 기존 모델 대비 성능 우수:
  • CIFAR-10에서 FID: 3.17.
  • LSUN-bedroom에서 FID: 2.92.

5.3 샘플 품질

• 고품질 샘플 생성:
  • 점진적으로 생성된 이미지는 선명하며 세부적인 구조를 잘 반영.

5.4 생성 속도

• Reverse Process는 단계별 진행 → 속도 느림.

---

6. 주요 기여 및 한계

6.1 주요 기여

1. 확률적 접근:
   • Forward와 Reverse 과정의 명확한 정의로 안정적 학습 가능.
2. 고품질 이미지 생성:
   • 기존 모델 대비 FID와 시각적 품질 모두 우수.
3. 생성 안정성:
   • GAN 대비 훈련 불안정성 문제 최소화.

6.2 한계

1. 속도:
   • 단계별 Reverse Process로 인해 계산 비용 증가.
2. 분산 모델링:
   • 현재 상수 분산을 사용 → 성능 개선 여지 존재.

---

7. 결론

 

• DDPM은 Forward와 Reverse 과정을 Markov Chain으로 정의하며, Gaussian 노이즈 추가 및 제거를 통해 데이터를 모델링.
• U-Net과 Reparameterization Trick을 활용하여 안정적 학습과 고품질 샘플 생성.
• Quadratic Noise Schedule은 유연성과 학습 효율성을 개선.
• DDPM은 기존 Generative 모델의 한계를 극복하며, 확률적 모델링을 통한 고품질 이미지 생성을 입증.
• 향후 연구 방향:
  • Reverse Process 속도 개선.
  • 다양한 태스크로의 확장.