[CV] 이론 정리

Theory/Computer Vision

[CV] 이론 정리

YeonJuJeon 2025. 2. 9. 17:34

▼ 1. 머신러닝

1. 머신러닝의 정의

인공지능(AI), 머신러닝(ML), 딥러닝(DL)의 관계:
- 머신러닝은 인공지능의 하위 개념.
- 딥러닝은 머신러닝의 하위 개념.
머신러닝:
- 데이터를 이용하여 신경망과 딥러닝을 통해 자율 학습.
- 명시적 프로그래밍 없이 학습 가능.

2. 머신러닝의 과정

데이터를 수집하고 전처리.
머신러닝 모델 학습.
손실함수를 최적화하여 모델 파라미터 찾기.
학습 완료 후 최적의 모델로 예측 및 응용.

2. 데이터의 종류

Training 데이터: 모델 훈련용 데이터.
Validation 데이터: 모델 최적화를 확인하기 위한 데이터.
Test 데이터: 최종 성능 검증용 데이터.

3. 머신러닝 주요 용어

데이터
- Label(Target): 예측하고자 하는 값 (예: y).
- Feature: 입력 변수 (예: x1,x2,…,xn).
모델: 데이터 기반 패턴 학습 및 예측/결정을 수행하는 알고리즘.
학습(Training):
- 데이터를 통해 모델의 최적 파라미터 탐색.
- 최적화를 통해 성능 개선.
모델 파라미터:
- 학습 과정에서 조정되는 내부 변수.
- 손실함수 최적화로 파라미터 조정.
- 예: m (기울기), b (절편).
손실함수:
- 모델 예측값과 실제 값의 차이를 측정하는 함수.
최적화:
- 손실함수를 최소화하는 수학적 과정.

4. 회귀(Regression)와 분류(Classification)

Regression(회귀): 연속적인 값을 예측.
- 예: 평균 기온 예측.
Classification(분류): 특정 카테고리를 예측.
- 예: 동물 이미지 분류.

5. Regression(회귀)의 종류

선형 회귀 (Linear Regression):
- 두 변수 간 선형 관계 분석.
- 왜 선형 회귀인가?
  - 데이터의 노이즈에도 불구하고 선형 관계를 유지.
  - 단순하지만 해석 가능성이 높음.
- 선형 모델의 구성
  - 모델:
  $$ F(m,b;x)=mx+b $$
  - 파라미터:
    - m: 기울기.
    - b: 절편.
  - 목표:
    - 손실함수 최적화를 통해 m, b를 조정.
로지스틱 회귀 (Logistic Regression):
- 0~1 사이의 확률 값으로 예측.

6. 최소 제곱법 (Least Squares) - 손실함수 최적화 방법

잔차제곱합 (RSS) - 손실함수:
- Residual(잔차): 예측 값과 실제 값의 차이.
$$ RSS = \sum_{i=1}^n (y_i - \hat{y}_i)^2
$$

$$ y_i: 실제값. $$

$$ \hat{y}_i: 모델 예측값. /수식 $$

최소화 조건 - RSS를 m과 b에 대해 편미분:

$$ \frac{\partial RSS}{\partial m} = 0, \quad \frac{\partial RSS}{\partial b} = 0 $$

편미분 계산:

$$ \frac{\partial RSS}{\partial m}: \frac{\partial}{\partial m} \sum_{i=1}^n \left( y_i - (mx_i + b) \right)^2 = -2 \sum_{i=1}^n x_i \left( y_i - (mx_i + b) \right) $$

$$ \frac{\partial RSS}{\partial b}: \frac{\partial}{\partial b} \sum_{i=1}^n \left( y_i - (mx_i + b) \right)^2 = -2 \sum_{i=1}^n \left( y_i - (mx_i + b) \right) $$

연립 방정식 - 위 두 식을 연립하여 m∗와 b∗를 구함:\sum_{i=1}^n y_i = m \sum_{i=1}^n x_i + nb $$
$$ \sum_{i=1}^n x_i y_i = m \sum_{i=1}^n x_i^2 + b \sum_{i=1}^n x_i $$
$$
최소 제곱 추정량(m와 b)의 계산 결과:

$$ 기울기 (m*):\frac{n \sum x_i y_i - \sum x_i \sum y_i}{n \sum x_i^2 - (\sum x_i)^2} $$

$$ 절편 (b*):\frac{\sum y_i - m^* \sum x_i}{n} $$

최적화 과정:
- RSS를 최소화하여 모델 파라미터 탐색.
한계:
- Outlier(이상치)에 민감.

▼ 2. 경사 하강법

1. 손실함수 복습

손실함수(Loss Function): 모델의 예측값과 실제값의 차이를 수치로 나타내는 함수.
- 예시: MSE, Cross-Entropy 등
최적화(Optimization): 손실함수를 최소화하기 위한 수학적 기법.
- 예시: 경사하강법, 최소제곱법

2. 경사하강법 (Gradient Descent)

목표: 손실함수의 최솟값을 찾아내는 것.
원리: 손실함수의 기울기를 계산하여 가장 가파르게 내려가는 방향으로 파라미터를 업데이트.
비유: 안개가 낀 산에서 산을 내려가는 과정처럼, 조금씩 방향을 조정하며 목적지에 도달.

경사하강법의 종료 조건

미분 계수가 0이 되는 지점(극소점)에 도달했을 때.
손실값이 일정 기준 이하로 작아지거나 더 이상 감소하지 않을 때.

다변수 함수에서의 적용

여러 변수에 대해 각각의 기울기를 계산하여 업데이트 진행.

3. Hyperparameter

경사하강법의 효율성과 정확도를 결정하는 중요한 요소들:
1. 학습률(Learning Rate): 파라미터가 업데이트되는 크기를 조정.
2. Batch 크기: 데이터를 몇 개씩 나눠서 학습할지 결정.
3. Epoch 수: 전체 데이터셋을 학습하는 횟수.

4. 경사하강법의 한계

계산량 문제: 데이터가 많아질수록 계산량이 급증.
Local Minimum 문제: 손실함수가 최솟값이 아닌 국소 최솟값에 갇힐 가능성.
Plateau 문제: 손실함수의 변화가 거의 없는 평탄한 구간에 빠질 위험.

▼ 3. 인공 신경망

1. 인공신경망(Neural Network, NN)의 정의

입력 데이터와 출력 데이터 사이의 관계를 수학적 함수로 모델링한 구조임.
뇌의 학습 과정을 컴퓨터에서 구현한 인공지능 모델임.

2. 신경망의 구성 요소

노드(Node): 입력 데이터와 가중치를 기반으로 연산을 수행하며, 결과를 다음 단계로 전달함.
1. 벡터 형식의 데이터 입력됨.
2. 입력값에 가중치가 곱해짐.
3. 활성화 함수를 통과하여 출력값을 생성함.
가중치(Weight): 데이터를 학습시키며 성능을 높이는 핵심 요소임.
계층(Layer): 다수의 노드가 연결된 형태로, 입력층(Input), 은닉층(Hidden), 출력층(Output)으로 구성됨.

3. 활성화 함수 (Activation Function)

1. 활성화 함수의 정의

비선형성을 도입하여 데이터의 복잡한 패턴을 학습 가능하게 만듦.
입력값을 그대로 전달하지 않고, 주로 비선형 함수를 통과시킴.

2. 활성화 함수의 종류

ReLU (Rectified Linear Unit)
- 특성: 음수를 0으로, 양수는 그대로 출력.
- 장점: 계산이 간단하며, 학습 속도를 빠르게 함.
- 단점: 음수 값에서는 기울기가 0이 되어 학습되지 않는 Dead Neuron 문제 발생 가능.
$$ f(x)=max(0,x) $$
Sigmoid
- 특성: 출력값을 (0, 1) 사이로 변환.
- 장점: 확률 기반 출력에 적합.
- 단점: 입력값이 크거나 작으면 기울기가 0에 가까워지는 Gradient Vanishing 문제가 발생.
$$ f(x) = \frac{1}{1 + e^{-x}} $$
Tanh (Hyperbolic Tangent)
- 특성: 출력값을 (-1, 1) 사이로 변환.
- 장점: Sigmoid보다 중심이 0에 가까워 학습 효율이 높음.
- 단점: Gradient Vanishing 문제가 여전히 존재.
$$ f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$
Leaky ReLU
- 특성: ReLU에서 음수 값 영역에 작은 기울기를 추가하여 Dead Neuron 문제를 완화.
- 일반적으로 α 값은 0.01로 설정.
$$ f(x) = \begin{cases} x, & \text{if } x > 0 \\ \alpha x, & \text{if } x \leq 0 \end{cases} $$
Softmax
- 특성: 모든 출력값을 (0, 1) 사이로 변환하며, 합이 1이 되도록 정규화.
- 주로 분류 문제의 출력층에 사용됨.
$$ f(x_i) = \frac{e^{x_i}}{\sum_{j=1}^N e^{x_j}} $$

활성화 함수의 선택 기준

ReLU: 기본값으로 자주 사용됨. 대부분의 은닉층에서 효율적.
Sigmoid/Tanh: 출력 값의 범위가 필요한 경우나 특정 문제에 적합.
Softmax: 다중 클래스 분류 문제의 출력층에서 필수적으로 사용.

4. 신경망의 학습 단계

1. 데이터 전처리:

신경망 학습의 첫 단계는 데이터 전처리로, 입력 데이터의 품질을 높이고 학습 안정성을 확보하는 과정임.

1.1. 데이터 정규화 및 스케일링

Feature Scaling: 입력 데이터의 스케일 차이를 줄여 학습 효율을 향상시킴.
1. Min-Max Scaling:
  - 데이터를 [0, 1] 범위로 변환.
  $$ x' = \frac{x - x_{\text{min}}}{x_{\text{max}} - x_{\text{min}}} $$
2. Standardization:
  - 평균 0, 표준편차 1로 변환.
  $$ x' = \frac{x - \mu}{\sigma} $$

1.2. 결측값 처리

비어 있는 데이터를 평균, 중앙값으로 대체하거나 알고리즘 기반으로 대체.

1.3. 데이터 증강

기존 데이터를 변형하여 학습 다양성을 확보함.
- 예: 이미지 좌우 반전, 크기 조절, 텍스트 동의어 대체.

1.4. 데이터 분리

데이터를 학습(Training), 검증(Validation), 테스트(Test) 세트로 분리.
- 일반 비율: 70:20:10 또는 80:10:10.

2. 신경망 모델 구성

레이어 구성:
- 입력층(Input Layer): 데이터의 특성을 모델에 전달.
- 은닉층(Hidden Layer): 패턴 학습과 복잡한 연산 수행.
- 출력층(Output Layer): 최종 결과 출력.
가중치 초기화:
- He Initialization, Xavier Initialization을 사용해 학습 속도와 안정성을 높임.
활성화 함수 선택:
- 예: Leaky ReLU, ReLU, Sigmoid, Tanh
  - Gradient Vanishing 문제

3. 손실 함수 정의 및 계산

손실 함수는 예측값과 실제값의 차이를 측정하여 모델의 성능을 평가.
손실 함수의 종류:
CEE: 분류 문제에서는 주로 정답(yi)을 one-hot encoding하며 출력층에서 softmax 함수와 같이 쓰임.

4. 손실 함수 최적화

Optimizer(최적화 기법):
- 손실값을 최소화하기 위해 가중치와 편향을 업데이트.
- 예: SGD, Adam, RMSprop.
학습률(Learning Rate):
- 가중치 업데이트 크기를 결정하며, 학습 속도와 안정성에 영향을 미침.

5. 순전파 (Forward Propagation)

입력 데이터가 네트워크를 통과하며 각 노드와 계층을 거쳐 최종 출력값을 생성.
과정:
1. 입력값에 가중치를 곱하고 편향을 더한 값을 각 노드에서 계산.
2. 활성화 함수를 통해 출력값을 다음 계층으로 전달.
3. 출력층에서 최종 예측값을 생성.

순전파 예시:

$$ X=[1,2,3,4], W=[5,6,7,8], b=1 $$

$$ Y = \phi(X \cdot W + b) = \phi(71) $$

6. 역전파 (Backward Propagation)

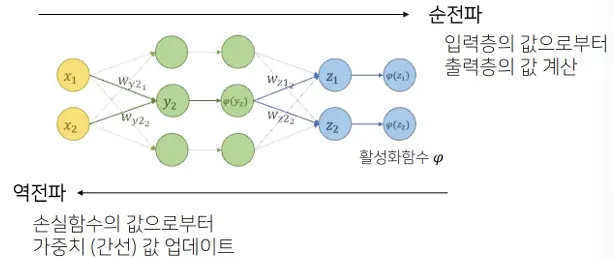
손실 함수의 기울기를 계산하여 가중치와 편향을 업데이트하는 과정.
연쇄 법칙(Chain Rule):
- 각 계층에서의 출력값이 이전 계층의 입력값에 의존하므로, 미분값을 계층별로 연쇄적으로 계산.
과정:
1. 출력층에서 손실 함수를 기준으로 오차 계산.
2. 오차를 기반으로 각 가중치와 편향에 대한 기울기(Gradient) 계산.
3. Optimizer를 사용해 가중치와 편향을 업데이트.

순전파와 역전파 간의 상호작용

순전파는 예측값을 생성하고, 역전파는 이를 바탕으로 모델을 개선함.
이 과정이 학습 반복(epoch) 동안 지속되며, 손실 값이 점차 감소하게 됨.

5. 하이퍼파라미터 (Hyperparameter)

학습 과정에서 설정해야 하는 값들로, 모델의 성능에 영향을 미침.
- Learning Rate: 가중치 업데이트 크기.
- Batch Size: 학습 시 사용하는 데이터의 묶음 크기.
- Epoch: 전체 데이터셋을 학습하는 횟수.

6. 신경망 학습의 전체 과정

데이터 전처리 및 모델 설정.
손실 함수 및 Optimizer 선택.
하이퍼파라미터 조정.
학습 종료 조건을 만족할 때까지 반복.

7. 요약

신경망은 수학적 모델을 기반으로 데이터 학습 및 예측을 수행함.
손실함수를 최소화하기 위해 순전파와 역전파를 반복하여 가중치를 업데이트함.
효율적인 학습을 위해 적절한 하이퍼파라미터와 Optimizer를 설정해야 함.

▼ 4. CNN

1. 컴퓨터가 이미지를 인식하는 방식

비트맵 이미지:
- 각 위치의 픽셀들이 색상 정보를 저장.
- 흑백 이미지: 픽셀 값이 0(검은색)에서 255(흰색) 사이로 표현.
- 컬러 이미지: RGB 채널로 구성, 각 채널의 값이 0~255로 표현됨.
이미지 데이터의 속성:
- 이미지는 3차원 배열로 표현 (Width × Height × Channel(=Depth)).

2. 밀집 신경망에서 CNN으로

밀집 신경망(DNN)은 입력 데이터를 1차원 벡터로 변환하여 학습.
이미지의 공간적 구조(Width, Height)를 반영하지 못함.
CNN은 공간적 정보를 유지하며 학습 가능하므로 이미지 처리에 적합.

3. CNN의 구조

CNN은 다음과 같은 계층으로 구성됨:

합성곱 계층 (Convolutional Layer):
- 이미지를 필터(Filter)로 스캔하여 특징을 추출.
- 필터 크기(Kernel Size), 스트라이드(Stride), 패딩(Padding) 등 하이퍼파라미터가 중요.
- 필터는 학습을 통해 최적화됨.
풀링 계층 (Pooling Layer):
- 데이터 크기를 줄이고 계산량을 감소시키며, 과적합 방지.
- 풀링 연산은 각 채널별로 독립적으로 수행됨.
- 종류:
  - 최대 풀링(Max Pooling): 영역 내 최대값 선택.
  - 평균 풀링(Average Pooling): 영역 내 평균값 선택.
밀집 계층 (Fully Connected Layer):
- 이미지 데이터를 1차원 벡터로 변환(Flatten)하여 분류나 예측 수행.

4. 합성곱 연산

필터(Filter):
- 입력 데이터에서 특정 특징을 추출하는 역할.
- 필터의 크기와 이동 간격(Stride)을 결정해야 함.
패딩(Padding):
- 가장자리 정보 손실을 방지하기 위해 입력 데이터 주변에 값(주로 0)을 추가.
- 패딩 종류:
  - Valid Padding: 패딩 없음.
  - Same Padding: 출력 크기를 입력 크기와 동일하게 유지.
편향(Bias):
- 합성곱 연산에 포함되어 필터 연산을 거친 출력에 동일하게 더함.
출력 크기 계산:
$$ \text{Output Size} = \frac{\text{Input Size} - \text{Filter Size} + 2 \times \text{Padding}}{\text{Stride}} + 1 $$

5. 다중 채널 이미지에 대한 합성곱 연산 정리

다중 채널 이미지와 합성곱 연산
- 컬러 이미지:
  - 일반적으로 RGB 채널로 구성되며, 각 채널이 독립적인 데이터를 가짐.
  - 예: 3개의 채널을 가진 (Width×Height×3) 크기의 데이터.
- 합성곱 연산의 조건:
  - 입력 데이터의 채널 수와 필터(Filter)의 채널 수는 동일해야 함.
  - 필터는 각 채널에 대해 독립적으로 가중치를 학습하고, 결과를 합산하여 출력값을 생성.
출력 채널이 여러 개인 경우
- 출력 채널 수를 늘리려면 필터 개수를 증가시켜야 함.
- 출력 채널 계산:
  - 입력 데이터의 채널 수와 관계없이 필터 개수가 출력 데이터의 채널 수를 결정.
  - 예:
    - 입력 데이터: (Width×Height×3) (채널 3개)
    - 필터: 3개의 채널을 가진 2개의 필터
    - 출력 데이터: (Width×Height×2) (채널 2개)
학습과정에서의 필터
- 필터의 역할:
  - 입력 데이터에서 특징을 추출.
  - 필터는 학습 과정에서 갱신되는 모델 파라미터로, 최적의 값을 찾아 학습됨.
- 출력 데이터:
  - 필터의 값에 따라 신경망의 최종 출력값이 달라짐.
  - 따라서 필터는 CNN 학습 과정에서 매우 중요한 요소임.
정리
- 입력 데이터의 채널 수는 필터의 채널 수와 같아야 함.
- 출력 데이터의 채널 수는 사용된 필터 개수에 의해 결정됨.
- 필터는 학습을 통해 갱신되며, 신경망이 데이터의 특징을 정확히 추출할 수 있도록 조정됨.

6. CNN 학습 과정

합성곱 계층:
- 필터를 학습하며 이미지의 특징을 추출.
활성화 함수 적용:
- 주로 ReLU(Rectified Linear Unit) 사용.
- 비선형성을 추가하여 복잡한 패턴 학습 가능.
풀링 계층:
- 데이터의 크기를 축소.
- 특징 유지 및 과적합 방지.
Flatten:
- 2차원 행렬 데이터를 밀집 계층에 전달하기 위해 1차원 벡터로 변환.
밀집 계층:
- 최종 분류나 예측 수행.
손실 함수 및 최적화:
- 손실 값을 기준으로 가중치와 편향을 업데이트.
- Optimizer 예: SGD, Adam.

7. AlexNet

등장 배경:
- 2012년 ILSVRC 대회에서 우승하며 CNN 대중화.
구조:
- 8개의 계층(5개의 합성곱 계층 + 3개의 밀집 계층).
- 드롭아웃(Dropout) 및 ReLU를 활용하여 과적합 방지와 학습 속도 향상.
출력 크기 계산:$$ W_{\text{out}} = \frac{W_{\text{in}} - W_{\text{filter}} + 2P}{S} + 1 $$
$$ H_{\text{out}} = \frac{H_{\text{in}} - H_{\text{filter}} + 2P}{S} + 1 $$

8. CNN 전체 흐름

입력 이미지 → 합성곱 계층 → 활성화 함수 → 풀링 계층 반복.
Flatten → 밀집 계층 → 최종 출력.
손실 함수와 역전파를 통해 필터와 가중치를 업데이트하며 학습.

▼ 5. Segmentation & Object Detection

Segmentation

정의: 이미지를 픽셀 레벨로 이해하는 접근법.
- 픽셀 하나하나에 분류 또는 탐지를 수행.
- 동일한 라벨을 가진 모든 픽셀이 동일한 객체 또는 클래스에 속하도록 픽셀에 라벨을 할당.
- 이미지 분류(image classification)보다 더 어려움.
- 활용 분야: 자율주행, 로봇공학, 의료 영상 분석 등.
입출력
- Input: RGB 또는 흑백 이미지.
- Output: 각 픽셀이 속하는 클래스를 나타내는 Map.

Segmentation 종류

Semantic Segmentation
- 같은 클래스 내의 인스턴스를 구별하지 않음.
Instance Segmentation
- 같은 클래스 내에서도 다른 인스턴스를 구분.

Semantic Segmentation 기법

1. 픽셀 기반 분류

모든 픽셀마다 개별적으로 분류.
정확하지만 계산량이 많아 비효율적.

2. Bilinear Interpolation

일부 픽셀만 학습하고 나머지는 추정.
장점: 계산량 감소, 학습 시간 단축.
단점: 정확도 감소 가능.

3. Convolution 기반 모델

문제점: 기존 모델(VGG, ResNet)은 위치 정보 손실.
해결: Downsampling, Upsampling 및 Encoder-Decoder 구조 사용.
- Encoder: 차원 축소.
- Decoder: 차원 복원.
  - Transpose Convolution
모델:
- FCN: VGG16을 전이 학습, Fully Connected Layer 제거, Fully Convolution Layer 대체, Transposed Convolution 통해 압축된 heat map을 확장, Skip Connection 적용하여 정보 전달.
- DeepLab: Dilated Convolution으로 FCN의 receptive field 문제 해결.
- U-Net: U자형 구조, Skip Connection 활용.

성능 평가 (Performance Measure)

IoU (Intersection over Union)
- 공통 영역과 전체 영역의 비율로 정확도 평가.
$$ IoU = \frac{\text{True Positive}}{\text{True Positive} + \text{False Positive} + \text{False Negative}} $$
PQ (Panoptic Quality):

Object Detection (객체 탐지)

정의
- 디지털 이미지와 비디오에서 특정한 객체 인스턴스(예: 인간, 자동차)를 감지하는 컴퓨터 기술.
- 주로 컴퓨터 비전, 이미지 처리와 관련.
- 주요 응용 분야: 얼굴 검출, 보행자 검출 등.
Object Detection vs. Image Classification
- Image Classification:
  - 이미지에 주 대상 물체가 하나만 있다고 가정.
  - 목표: 대상 물체의 카테고리를 식별.
- Object Detection:
  - 이미지에 하나 이상의 대상이 존재.
  - 목표: 대상의 카테고리와 위치를 특정.
  - 동시에 분류(Classification)와 회귀(Regression)를 수행.
Output 예시
- Bounding Box 좌표 (x, y, w, h) 및 클래스 레이블과 확률.
  - x, y: 경계 박스 중심점.
  - w, h: 경계 박스의 너비와 높이.

Object Detection Pipeline

입력 이미지 (Input Image):
- 디지털 이미지 또는 비디오 프레임.
- 예: 고양이, 개, 자동차 등 다양한 객체 포함.
Pretrained Feature Extractor:
- 모델:
  - VGG, ResNet 등 사전 학습된 CNN 사용.
  - MS COCO, ImageNet과 같은 데이터셋으로 학습됨.
- 기능:
  - 객체의 특징 맵(Feature Map)을 생성.
  - 일반화 성능이 높은 이미지 분류 모델 선택.
Region Proposal (영역 제안):
- 목적:
  - 객체가 있을 가능성이 높은 관심 영역(ROI)을 선택.
- 기법:
  - RPN (Region Proposal Network).
  - Selective Search.
  - Sliding Window.
Object Detection Network:
- 구조:
  - Fully Connected Layer (fc-layer) 포함.
- 물체를 감싸는 **경계 박스(Bounding Box)**를 예측.
  - 좌표: x,y,w,h.
  - x, y: 중심점 좌표.
  - w, h: 너비와 높이.
- Classification:
  - 각 객체의 클래스와 확률 (Softmax 사용).

Object Detection 알고리즘

Region Proposal (영역 제안)
- 객체가 있을 가능성이 높은 영역(Region)을 후보로 추출.
- 방법:
  - Sliding Window:
    - 윈도우를 이미지 상단에서 하단으로 이동하며 Region을 탐색.
    - 단점: 계산 비용 높음, 정확도 낮음.
  - Selective Search:
    - 컬러, 크기, 형태 기반으로 유사한 영역을 그룹화.
    - 최적의 Bounding Box를 선택.
  - RPN (Region Proposal Network):
    - CNN으로 특징 맵을 추출하여 객체 존재 확률과 경계를 예측.
    - 학습 가능한 네트워크로 효율적 탐색 가능.
1-Stage Detector vs. 2-Stage Detector
- 1-Stage Detector:
  - Region Proposal과 Classification을 동시에 수행.
  - YOLO, SSD.
  - 특징: 빠른 속도.
- 2-Stage Detector:
  - Region Proposal과 Classification을 순차적으로 수행.
  - R-CNN, Fast R-CNN, Faster R-CNN.
  - 특징: 높은 정확도.
Non-Maximum Suppression (NMS)
- 동일 객체를 여러 박스로 탐지하는 문제 해결.
- 높은 Objectness Score를 가진 박스만 유지, 나머지를 제거.
- 기준:
  - Confidence Score: 0.6
    - 특정 바운딩 박스안에 있는 객체가 어떤 물체의 클래스일 확률
    - Softmax 단계로 도출된 확률값 X IoU
    - 즉, 각 바운딩 박스안에 물체가 있을 확률
  - IoU (Intersection over Union): 0.5
    - 두 박스의 중첩률 계산 (0~1 범위).
    - 중첩률은 정확한 예측을 정의하는 용도로 사용됨.
      - 중첩률이 설정된 임계값보다 크면 정확한 예측이 됨을 의미함.
      - 일반적으로 0.5가 많이 사용됨.
평가 지표
- mIoU:
  - 모든 클래스에 대한 각 Object에 그려지는 모든 Bounding Box의 IoU를 평균낸 것.
- mAP (mean Average Precision):
  - 모든 클래스에 대해 PR 곡선을 구해 AP를 계산.
  - 각 클래스의 AP 평균값을 mAP로 계산.
    - mAP 계산 방법
      1. 각 Bounding Box와 Confidence Score 계산.
      2. Precision과 Recall 계산.
      3. PR 곡선 작성.
      4. 곡선 아래 면적(AP) 계산.
      5. 모든 클래스에 대해 AP 평균값(mAP) 계산.

mAP - Precision과 Recall 조정

Precision 정의:
- 모델이 "사과"라고 예측한 것 중 실제로 "사과"인 비율.
$$ \text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} $$
Precision을 100%로 올리는 방법:
- 모델이 "틀린 예측(FP)"이 없도록 조정.
- 예시:
  1. 사과 10개, 배 10개가 주어진 상황.
  2. 모델이 "사과"라고 예측한 것 중 9개가 실제 사과, 1개가 배인 경우:
  3. $$ Precision = \frac{9}{10} = 90\% $$
  4. Precision 100%를 위해:
    - 모델이 확실한 사과 5개만 예측하고, 나머지 사과와 배를 "사과가 아니다"로 분류.
    $$ Precision = \frac{5}{5} = 100\% $$
- 문제점:
  - 많은 "사과"를 놓쳐 Recall(실제 사과를 찾아내는 능력)이 낮아짐.
Recall 정의:
- 실제 "사과" 중에서 모델이 "사과"라고 올바르게 예측한 비율.
$$ \text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} $$
Recall을 100%로 올리는 방법:
- 모든 "사과"를 놓치지 않도록 조정.
- 예시:
  1. 사과 10개, 배 10개가 주어진 상황.
  2. 모델이 실제 사과 9개를 "사과"라고 예측, 1개를 배로 예측한 경우:
  3. $$ Recall = \frac{9}{10} = 90\% $$
  4. Recall 100%를 위해:
    - 모델이 사과 10개와 배 10개 모두를 "사과"라고 예측.
    $$ Recall = \frac{10}{10} = 100\% $$
- 문제점:
  - 배도 "사과"로 잘못 예측하여 Precision이 낮아짐.

mAP - Precision-Recall (PR) 곡선

정의:
- Precision과 Recall 간의 관계를 그래프로 표현.
- 목적:
  - Precision과 Recall의 변화 추적.
  - 모델 성능 평가.
PR 곡선 작성 과정:
- True Positive (TP)와 False Positive (FP)를 계산.
- 모든 예측에 대해 Precision과 Recall을 계산.
- 계산된 값으로 PR 곡선을 그림.
PR 곡선의 의미:
- Recall이 증가해도 Precision이 감소하지 않으면 성능이 뛰어나다는 의미.
- PR 곡선 아래 면적(AP, Average Precision)을 계산하여 모델 성능 평가.

발전 과정

▼ 6. GAN

GAN (Generative Adversarial Networks)

https://ahxlzjt.tistory.com/16

정의:
- GAN: Generative Adversarial Nets.
- 이미지를 생성하기 위한 인공지능 모델.
구조:
- Generator (생성자):
  - 노이즈(Latent Vector)를 입력으로 받아 훈련 데이터와 유사한 데이터를 생성.
- Discriminator (판별자):
  - 입력 데이터가 진짜(Real)인지 가짜(Fake)인지 판별.
비유:
- 위조 지폐 사례:
  - Generator: 위조 지폐 제작.
  - Discriminator: 위조 지폐 감별.

GAN의 작동 원리

입력 및 출력:
- Fake: D(G(z))=0 (가짜 이미지).
- Real: D(x)=1 (진짜 이미지).
- z: 노이즈 벡터.
- x: 실제 데이터.

Loss Function

전체 목표:
- GAN은 **Generator (G)**와 **Discriminator (D)**가 서로 경쟁하는 구조로 학습.
- Generator는 Discriminator를 속이는 방향으로 학습하고, Discriminator는 진짜와 가짜를 구분하는 방향으로 학습.
Discriminator의 손실 함수:
- 목표:
  - 진짜 데이터를 1로, 가짜 데이터를 0으로 정확히 분류.
- 수식:
  - x: 실제 데이터.
  - z: 랜덤 노이즈 (Latent Vector).
  - D(x): Discriminator가 실제 데이터를 진짜로 예측한 확률.
  - D(G(z)): Discriminator가 Generator가 만든 가짜 데이터를 진짜로 예측한 확률.
- $$ L_D = - \mathbb{E}{x \sim p{\text{data}}(x)}[\log D(x)] - \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))] $$
- 해석:
  - 첫 번째 항: Discriminator가 진짜 데이터를 진짜로 판별하는 손실.
  - 두 번째 항: Discriminator가 가짜 데이터를 가짜로 판별하는 손실.
Generator의 손실 함수:
- 목표:
  - Generator가 생성한 가짜 데이터를 Discriminator가 진짜로 판단하게끔 속임.
- 수식:
  - G(z): Generator가 생성한 가짜 데이터.
  - D(G(z)): Discriminator가 가짜 데이터를 진짜로 판별한 확률.
- $$ L_G = - \mathbb{E}_{z \sim p_z(z)}[\log D(G(z))] $$
- 해석:
  - Generator는 D(G(z))가 높아지도록 (즉, Discriminator가 속도록) 학습.
미니맥스 게임 형태:
- GAN의 전체 학습 과정은 미니맥스 게임으로 정의.
- 목표 수식:
  - Generator는 손실을 최소화(minG).
  - Discriminator는 손실을 최대화(maxD).
- $$ \min_G \max_D V(D, G) = \mathbb{E}{x \sim p{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))] $$
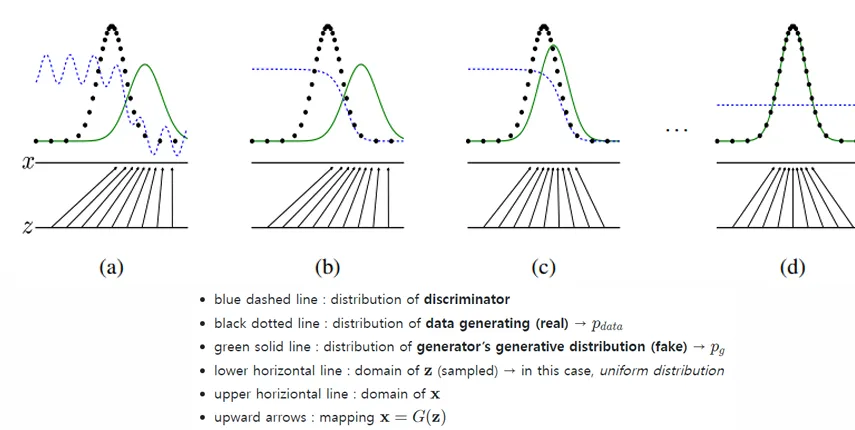
수렴 시 결과:
- Generator가 이상적으로 학습되면, Generator가 만든 가짜 데이터의 분포가 실제 데이터의 분포와 동일해짐:
  - D(x)≈0.5 (진짜와 가짜를 구분할 수 없음).
- 이때 V(D,G)의 최적값은 −log(4).

왜 Loss Function이 중요한가?

Generator와 Discriminator의 균형:
- Generator와 Discriminator가 너무 강하거나 약하면 학습이 불안정.
  - Discriminator가 너무 강하면 Generator가 학습하지 못함.
  - Generator가 너무 강하면 Discriminator가 가짜를 구분하지 못함.
학습 안정성 문제:
- GAN은 훈련 초기에는 Loss가 명확히 감소하지 않을 수 있음.
- 이를 해결하기 위해 DCGAN에서는 Batch Normalization, Strided Convolutions 등이 도입됨.

GAN의 구성 요소

1. Generator:

목표: 노이즈 벡터를 훈련 데이터의 분포와 비슷하게 변환.

구조:
- Fully Connected Layer (FCN).
- 활성화 함수: ReLU.
- 데이터 변환 후 이미지 생성.

2. Discriminator:

목표: 입력 데이터가 Real(1)인지 Fake(0)인지 분류.
구조:
- Fully Connected Layer (FCN).
- 활성화 함수: ReLU 및 Sigmoid.
- 출력: 0 또는 1.

3. 학습 방식:

Discriminator: 지도 학습(Supervised Learning).
Generator: 비지도 학습(Unsupervised Learning).

DCGAN (Deep Convolutional GAN)

https://ahxlzjt.tistory.com/40

DCGAN의 특징:
- G와 D에서 Fully Connected Layer(FCN) 대신 Convolution Layer 사용.
- Pooling Layer를 사용하지 않고, Strided Convolutions로 대체.
- Batch Normalization을 사용하여 학습 안정화.
- CNN 구조로 공간 정보를 학습하여 연속적인 이미지 생성 가능.
Generator 구조:

Upconvolution → BatchNorm → ReLU → 이미지 출력.

3. Discriminator 구조:

Convolution → BatchNorm → ReLU → Sigmoid → 0 또는 1 출력.

'Theory > Computer Vision' 카테고리의 다른 글

[의학영상처리] 정리본 (0)	2025.02.09

현재글[CV] 이론 정리

연주의 공부 기록

Medical Image AI & CV 내가 보려고 만든 블로그💻 논문 & 코드 리뷰 및 이론 정리. * 논문 리뷰 요약은 흐름 파악용.

transformer, regression, RNN, 의학영상처리, srdiff, voxelmorph, LSTM, maisi, instantstyle, sr3, votenet, gpt-neox-20b, pytorch, keras, fami, Distillation, ip-adapter, classification, deep-emotion, sleap,

Today :
Yesterday :

일	월	화	수	목	금	토
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28

[CV] 이론 정리

▼ 1. 머신러닝

1. 머신러닝의 정의

2. 머신러닝의 과정

2. 데이터의 종류

3. 머신러닝 주요 용어

4. 회귀(Regression)와 분류(Classification)

5. Regression(회귀)의 종류

6. 최소 제곱법 (Least Squares) - 손실함수 최적화 방법

▼ 2. 경사 하강법

1. 손실함수 복습

2. 경사하강법 (Gradient Descent)

경사하강법의 종료 조건

다변수 함수에서의 적용

3. Hyperparameter

4. 경사하강법의 한계

▼ 3. 인공 신경망

1. 인공신경망(Neural Network, NN)의 정의

2. 신경망의 구성 요소

3. 활성화 함수 (Activation Function)

4. 신경망의 학습 단계

5. 하이퍼파라미터 (Hyperparameter)

6. 신경망 학습의 전체 과정

7. 요약

▼ 4. CNN

1. 컴퓨터가 이미지를 인식하는 방식

2. 밀집 신경망에서 CNN으로

3. CNN의 구조

4. 합성곱 연산

5. 다중 채널 이미지에 대한 합성곱 연산 정리

6. CNN 학습 과정

7. AlexNet

8. CNN 전체 흐름

▼ 5. Segmentation & Object Detection

Segmentation

Segmentation 종류

Semantic Segmentation 기법

성능 평가 (Performance Measure)

Object Detection (객체 탐지)

Object Detection Pipeline

Object Detection 알고리즘

mAP - Precision과 Recall 조정

mAP - Precision-Recall (PR) 곡선

발전 과정

▼ 6. GAN

GAN (Generative Adversarial Networks)

GAN의 작동 원리

Loss Function

왜 Loss Function이 중요한가?

GAN의 구성 요소

DCGAN (Deep Convolutional GAN)

'Theory > Computer Vision' 카테고리의 다른 글

'Theory/Computer Vision'의 다른글

관련글

티스토리툴바