1. 데이터 로드 및 전처리
(1) Google Drive 연동 & CSV 파일 로드
import pandas as pd
import numpy as np
np.set_printoptions(suppress=True) # 지수표현(e) 대신 일반 숫자로 표현
from google.colab import drive
drive.mount('/content/drive')
dir_path = '/content/drive/MyDrive/Colab Notebooks/1_Code_OUTTA/1_Alpha_ML_TO_DL_241208/1_Shared_Alpha_ML_TO_DL/4_Alpha_Machine_Learning/4_ML_Resources/Resources/12_회귀모델_데이터/'
data = pd.read_csv(dir_path + 'HousingData.csv')
data- Google Colab에서 drive.mount()를 통해 Google Drive를 연동한다.
- read_csv로 주택 가격 예측용 CSV 데이터를 불러온다.
(2) 결측치 제거 후 train/test 분리
from sklearn.model_selection import train_test_split
df = data[:].dropna() # 결측치 제거
x_train, x_test, y_train, y_test = train_test_split(
df.drop('MEDV', axis=1),
df['MEDV']
)
x_train.shape, x_test.shape- dropna()로 결측치가 있는 행을 제거한다.
- train_test_split으로 독립변수(X)와 종속변수(Y)를 학습용/테스트용으로 분리.
- 여기서는 stratify 옵션을 사용하지 않는다(회귀 문제이므로 분류와 달리 클래스 분포가 필요 없음).
2. 회귀 모델 성능평가 지표
(1) MSE, MAE, RMSE 직접 구현 예시
pred = np.array([3,4,5])
actual = np.array([1,2,3])
def my_mse(pred, actual):
return ((pred - actual) ** 2).mean()
def my_mae(pred, actual):
return (np.abs(pred - actual)).mean()
def my_rmse(pred, actual):
return np.sqrt(my_mse(pred, actual))
print("MSE:", my_mse(pred, actual))
print("MAE:", my_mae(pred, actual))
print("RMSE:", my_rmse(pred, actual))- MSE(Mean Squared Error): $\frac{1}{n}\sum (y_i - \hat{y}_i)^2$
- MAE(Mean Absolute Error): $\frac{1}{n}\sum |y_i - \hat{y}_i|$
- RMSE(Root MSE): $\sqrt{MSE}$
(2) scikit-learn 활용
from sklearn.metrics import mean_absolute_error, mean_squared_error
print("MAE(sklearn):", mean_absolute_error(pred, actual))
print("MSE(sklearn):", mean_squared_error(pred, actual))- 직접 구현 대신 sklearn.metrics에 내장된 함수를 사용할 수 있다.
3. 모델별 성능 확인 함수
아래 두 함수는 그래프 시각화 및 MSE 비교를 도와준다.
import matplotlib.pyplot as plt
import seaborn as sns
my_predictions = {} # 각 모델의 mse를 담을 dict
def plot_predictions(name_, pred, actual):
df = pd.DataFrame({'prediction': pred, 'actual': actual})
df = df.sort_values(by='actual').reset_index(drop=True)
plt.figure(figsize=(12, 9))
plt.scatter(df.index, df['prediction'], marker='x', color='r')
plt.scatter(df.index, df['actual'], alpha=0.7, marker='o', color='black')
plt.title(name_, fontsize=15)
plt.legend(['prediction', 'actual'], fontsize=12)
plt.show()
def mse_eval(name_, pred, actual):
global my_predictions
# 예측값 vs 실제값 그래프
plot_predictions(name_, pred, actual)
# MSE 계산
mse = mean_squared_error(pred, actual)
my_predictions[name_] = mse # 딕셔너리에 저장
# 저장된 모델들의 MSE 순서대로 출력
y_value = sorted(my_predictions.items(), key=lambda x: x[1], reverse=True)
df = pd.DataFrame(y_value, columns=['model', 'mse'])
print(df)
# 수평 바 차트로 출력
min_ = df['mse'].min() - 10
max_ = df['mse'].max() + 10
length = len(df)
plt.figure(figsize=(10, length))
ax = plt.subplot()
ax.set_yticks(np.arange(len(df)))
ax.set_yticklabels(df['model'], fontsize=15)
bars = ax.barh(np.arange(len(df)), df['mse'])
# 각 바 위에 수치 표시
for i, v in enumerate(df['mse']):
ax.text(v + 2, i, str(round(v, 3)), color='k', fontsize=15, fontweight='bold')
plt.title('MSE Error', fontsize=18)
plt.xlim(min_, max_)
plt.show()
결과:
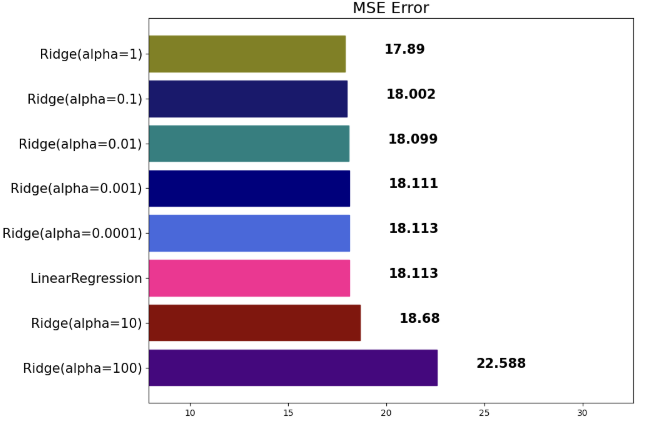

4. LinearRegression (기본 선형 회귀)
from sklearn.linear_model import LinearRegression
model = LinearRegression(n_jobs=-1)
model.fit(x_train, y_train) # 학습
pred = model.predict(x_test) # 예측
mse_eval('LinearRegression', pred, y_test)- LinearRegression은 가중치(계수)에 대한 규제가 없다 → 복잡한 데이터의 경우 과대적합 우려가 있음.
- n_jobs=-1은 CPU 코어를 전부 활용하겠다는 의미(병렬처리).
5. 규제(Regularization)
학습이 과대적합되는 것을 방지하기 위해 벌칙(패널티)을 부여해 가중치를 조정한다.
- L2 규제(릿지, Ridge)
-
$Error=MSE+αw^2$
-
- L1 규제(라쏘, Lasso)
-
$Error=MSE+α|w|$
-
L2 규제가 L1 규제에 비해 안정적이라 일반적으로 L2 규제가 더 많이 사용
(1) 릿지(Ridge) - L2 규제
from sklearn.linear_model import Ridge # sklearn.linear_model 안에 있음.
alphas = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001]
for alpha in alphas:
ridge = Ridge(alpha=alpha)
ridge.fit(x_train, y_train)
pred = ridge.predict(x_test)
mse_eval(f'Ridge(alpha={alpha})', pred, y_test)- $\alpha$ 가 클수록 규제가 강해져 가중치 절댓값이 작아진다.
- 과대적합 위험이 줄어들지만, $\alpha$ 가 너무 크면 과소적합이 될 수 있다.
(1) 계수 시각화
def plot_coef(columns, coef):
coef_df = pd.DataFrame(list(zip(columns, coef)), columns=['feature', 'coef'])
coef_df = coef_df.sort_values('coef', ascending=False).reset_index(drop=True)
fig, ax = plt.subplots(figsize=(9, 7))
ax.barh(np.arange(len(coef_df)), coef_df['coef'])
ax.set_yticks(np.arange(len(coef_df)))
ax.set_yticklabels(coef_df['feature'])
plt.show()
ridge_100 = Ridge(alpha=100)
ridge_100.fit(x_train, y_train)
plot_coef(x_train.columns, ridge_100.coef_)- plot_coef 함수로 가중치(계수)를 어떤 feature가 얼마나 받았는지 시각화해볼 수 있다.

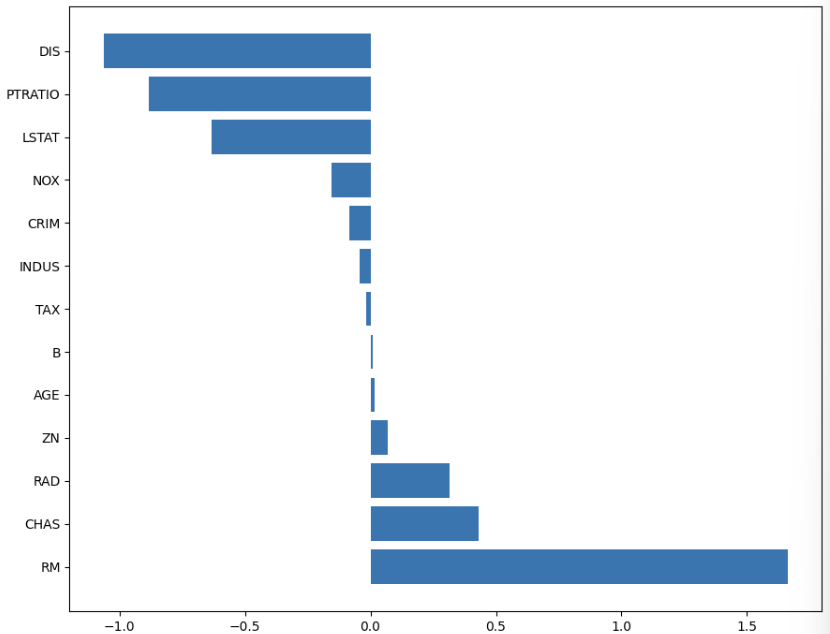

(2) 라쏘(Lasso) - L1 규제
from sklearn.linear_model import Lasso
alphas = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001]
for alpha in alphas:
lasso = Lasso(alpha=alpha)
lasso.fit(x_train, y_train)
pred = lasso.predict(x_test)
mse_eval(f'Lasso(alpha={alpha})', pred, y_test)- L1 규제는 가중치의 절댓값 합에 $\alpha$ 를 곱하여 추가.
- 일부 계수는 0으로 수렴 → 변수 선택(Feature Selection) 효과가 있다.

(3) 엘라스틱넷(ElasticNet) - L1 + L2 혼합
from sklearn.linear_model import ElasticNet
ratios = [0.2, 0.5, 0.8]
for ratio in ratios:
elasticnet = ElasticNet(alpha=0.5, l1_ratio=ratio)
elasticnet.fit(x_train, y_train)
pred = elasticnet.predict(x_test)
mse_eval(f'ElasticNet(l_ratio={ratio})', pred, y_test)- l1_ratio=0 → Ridge와 동일, l1_ratio=1 → Lasso와 동일.
- 0 < l1_ratio < 1이면 L1과 L2 규제가 혼합되어 적용된다.

6. 스케일러(Scaler)
데이터 전처리 단계에서 규모가 다른 숫자들을 비교하기 위해 정규화(Normalization)나 표준화(Standardization)를 적용한다.
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler
# sklearn.preprocessing 안에 있음.
x_train.info()
x_train.describe()- 데이터의 요약 통계를 확인(info, describe).

(1) StandardScaler
std_scaler = StandardScaler()
std_scaled = std_scaler.fit_transform(x_train)
round(pd.DataFrame(std_scaled).describe(), 2)- 평균을 0, 표준편차를 1로 맞춰준다.
(2) MinMaxScaler
minmax_scaler = MinMaxScaler()
minmax_scaled = minmax_scaler.fit_transform(x_train)
round(pd.DataFrame(minmax_scaled).describe(), 2)- 최소값을 0, 최대값을 1로 매핑한다.
(3) RobustScaler
robust_scaler = RobustScaler()
robust_scaled = robust_scaler.fit_transform(x_train)
round(pd.DataFrame(robust_scaled).median(), 2)- 중앙값을 0, IQR(interquartile range: 데이터의 중간 50%)를 1로 조정 → 이상치(Outlier) 상대적으로 강건(robust)하다.
- 중앙화(centering)하여 이상치의 영향을 최소화한다.
7. 파이프라인(Pipeline)
여러 처리 단계를 묶어서 한 번에 실행할 수 있다.
fit(훈련) 시점에 x와 y를 모두 요구한다(전처리 단계에서 y를 쓰지 않지만 모델 학습 단계에서 y가 필요하기 때문).
from sklearn.pipeline import make_pipeline # sklearn.pipeline 안에 make_pipeline 사용.
elastic_pipeline = make_pipeline(
StandardScaler(),
ElasticNet(alpha=0.1, l1_ratio=0.2)
)
model = elastic_pipeline.fit(x_train, y_train)
prediction = model.predict(x_test)
mse_eval('Standard ElasticNet', prediction, y_test)- StandardScaler로 스케일링 후, ElasticNet을 적용하는 전체 흐름을 파이프라인으로 정의.
- 파이프라인을 통해 데이터 전처리와 모델 훈련을 한 번에 관리할 수 있다.

8. Polynomial Features (다항 특성)
비선형 관계를 모델링하기 위해 다항식 항을 생성한다. (2개의 feature가 존재할 때, degree=2로 설정해본다.)
Ex) 2차 다항식이라면, 기존 $[x_1, x_2]$에서 $[1, x_1, x_2, x_1^2, x_1x_2, x_2^2]$를 추가로 만든다.
from sklearn.preprocessing import PolynomialFeatures # sklearn.preprocessing 안의 PolynominalFeatures을 사용.
poly = PolynomialFeatures(degree=2, include_bias=False)
poly_features = poly.fit_transform(x_train)[0]
print(poly_features) # 첫 번째 샘플 기준으로 변환된 다항 특성
print(x_train.iloc[0])- include_bias=False → 1(절편 항)은 생성하지 않는다.
- include_bias=True → 0(0차항)은 만든다.

(1) 다항 특징 + 스케일링 + 규제 결합 파이프라인
from sklearn.pipeline import make_pipeline
poly_pipeline = make_pipeline(
PolynomialFeatures(degree=2, include_bias=False),
StandardScaler(),
ElasticNet(alpha=0.1, l1_ratio=0.2)
)
poly_pred = poly_pipeline.fit(x_train, y_train).predict(x_test)
mse_eval('Poly ElasticNet', poly_pred, y_test)- 다항식 변환 → 표준화 → ElasticNet 순으로 진행.
- 다항식 변환 시, 과적합 위험이 커지므로 일반적으로 규제(Ridge/Lasso/ElasticNet)와 함께 쓰는 경우가 많다.

정리
- MSE/MAE/RMSE 등 회귀 모델 평가 지표는 필수.
- 릿지(Ridge), 라쏘(Lasso), 엘라스틱넷(ElasticNet)을 통해 가중치를 규제한다.
- $\alpha$가 크면 규제가 강해짐 → 과대적합 방지.
- $\alpha$가 너무 크면 과소적합 될 수도 있음.
- 스케일링(Scaling)은 전처리에서 중요한 역할(특히 규제 회귀나 거리기반 알고리즘에서: 정규화, 표준화).
- 파이프라인(Pipeline)으로 전처리와 모델 학습을 합쳐 관리하면 코드 간결화와 실수 방지에 효과적.
- PolynomialFeatures로 비선형성을 모델링하되, 차원이 커질 수 있어 규제와 함께 사용해야 적절한 성능을 낼 수 있음.